Dial In Your DCS Risk with the Thalmann Algorithm

By Tim Blömeke

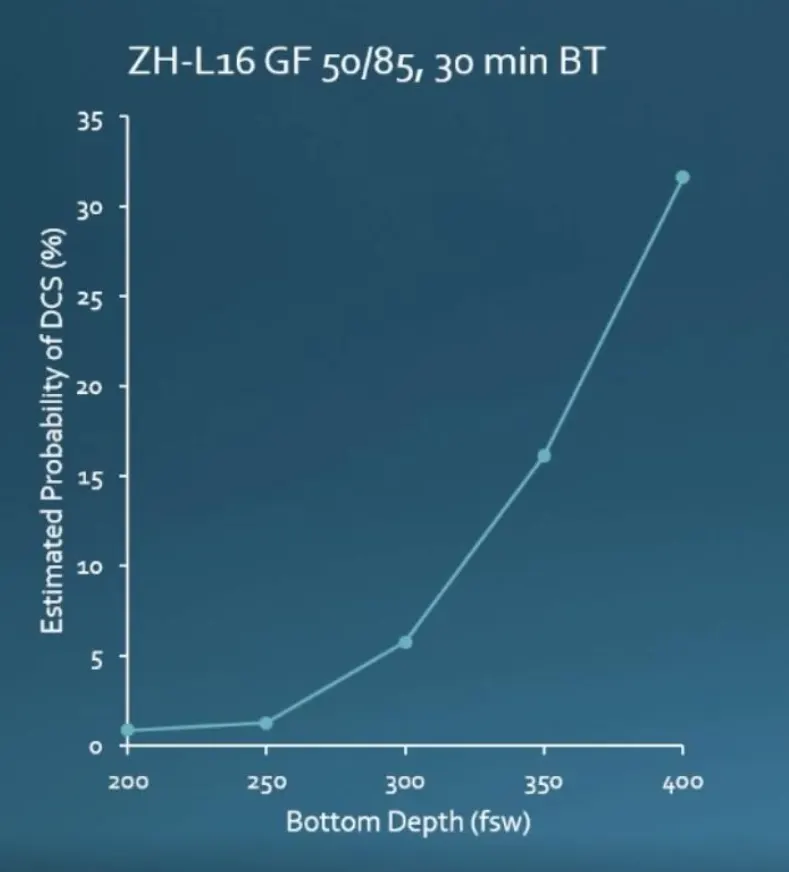
Dr. David Doolette’s lecture on Advances in Decompression Theory and Practice was among the most anticipated presentations of last year’s Rebreather Forum 4 (RF4). Toward the end of the linked video (starting at about 47:00), Doolette spent a few minutes explaining how deco schedules generated by Bühlmann-based models produce an escalating risk of decompression sickness (DCS) for dives with greater inert gas exposure. That is, a profile for a 100 m/330 ft dive with 30 minutes of bottom time will have a greater risk of DCS than a profile for a 70 m/230 ft dive with 20 minutes of bottom time generated with the same parameter settings (e.g., gradient factors).

Divers who wish to conduct very long and deep dives are, therefore, faced with a conundrum: In order to limit their DCS risk to a reasonable level, they will probably need to adjust the conservatism of their deco schedules relative to what commonly available deco algorithms suggest. The correct amount of such an adjustment, however, is anybody’s guess, since such dives lie outside the range of profiles for which the models have been validated. Or, as Kevin Gurr put it here in InDEPTH, “[…] Much of the deeper diving we do is simply an extrapolation of the early shallow water research. We now know that this does not always work.”

A more desirable state of affairs, said Doolette, would be to apply an iso-risk decompression model—that is, a model that generates deco schedules which hold the DSC risk constant across varying ranges of depth and bottom time. Finally, he suggested that such a model already exists and encouraged divers and researchers to look into the Thalmann decompression algorithm when planning big dives.

What is the Thalmann algorithm?

The Thalmann Exponential-Linear Decompression Algorithm isn’t new. It was first published in 1983 by U.S. Navy Captain Ed Thalmann for decompression for dives on the Mk-15 rebreather with a constant PO₂ of 0.7 ATA along with a FORTRAN code that could run on the Orca EDGE portable dive computer employed by the Navy at the time. It is a gas-content decompression model, as pioneered by Haldane and refined by Workman and Bühlmann, with nine tissue compartments in the original version.

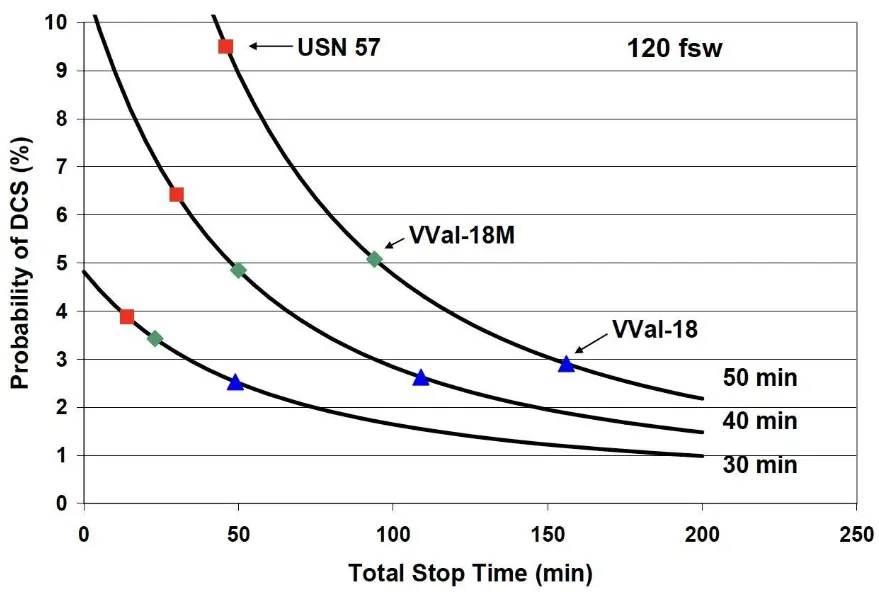
Twenty-five years later, after additional research and various modifications, the US Navy adopted the Thalmann algorithm as its standard decompression algorithm with the introduction of Revision 6 of its Diving Manual. It was this algorithm that was matched up against a VPM-based approach in the much-discussed U.S. Navy Experimental Diving Unit (NEDU) Deep Stops study.
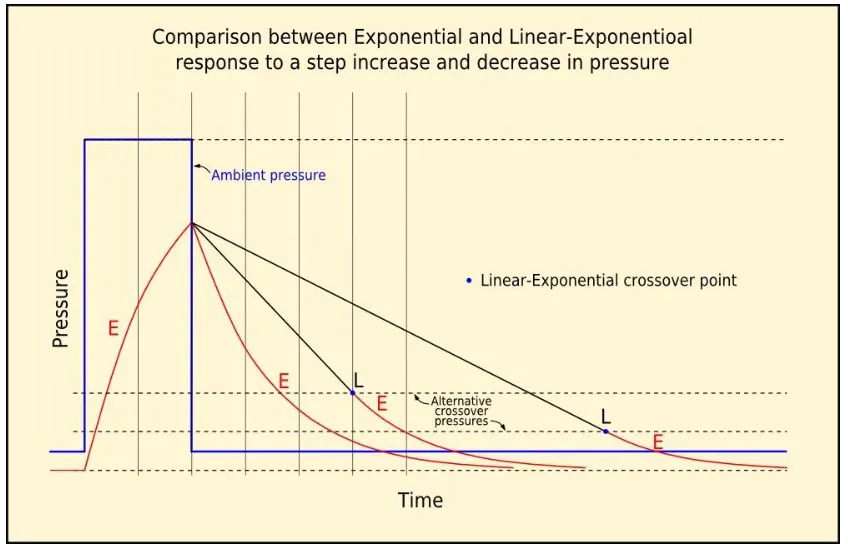
While Thalmann deco has much in common with other neo-Haldanean models, there is a key difference: Conventional models assume that the kinetics for on-gassing and off-gassing (or gas uptake and washout, in USN parlance) are symmetrical and governed by the same fundamental principle—an exponential decay function with a set of time constants to represent various theoretical tissue compartments. The Thalmann model, on the other hand, treats uptake and washout kinetics as dissimilar: While gas uptake is still represented as exponential, the washout is modeled by a function with a linear component. This means that gas washout is treated as a slower process than gas uptake.

This may seem counterintuitive at first glance: If you put a bowl of water in a pressure chamber to experimentally determine the rates of gas going into and coming out of solution, the two processes appear symmetrical and can be described by a single exponential function. Accordingly, when developing the programming for the U.S. Navy dive computer, the researchers initially used an exponential function to model both the uptake and washout processes, just as the creators of prior Haldanean models had done.

P_tissue(t) = P₀ + ∆P (1 – e ^{–ln(2) t/T}), with 

• t as the length of the time interval under consideration
• T as the tissue half-time

• P₀ as the tension (pressure) of dissolved gas at the start of the time interval
• ∆P as the difference between the tension of dissolved gas and the external pressure of gas
• P_tissue as the tension of dissolved gas at the end of the time interval
  

When the algorithm was tested experimentally on human subjects, Navy researchers found that it produced an unacceptably high incidence of symptomatic DCS for longer, deeper dives. However, changing the parameters governing the M-values in order to produce more conservative profiles for longer, deeper dives would have resulted in shorter no-stop times for dives that were already known from experience to be within the acceptable safety margin. The researchers subsequently found that tweaking the model by inserting a linear component into the modeling of the washout phase produced the desired result: a better approximation of the complex physiology of off-gassing and a means of generating profiles that met safety requirements for dives with greater exposure without being overly restrictive for lesser exposures.

The linear function (P_tissue = P₀ + bt) is applied for the washout process if (and as long as) the tissue supersaturation is above a defined crossover pressure (see fig. 3). The slope (b) of this linear function is equal to the gradient at which an exponential function (see above) would intersect with the crossover pressure line. 

Maybe it was this experience that inspired Ed Thalmann when he wrote, somewhat wistfully, “While many decompression models start out as mechanistic [i.e., designed to accurately model physiological processes (ed.)], they usually end up as mathematical [a set of equations bearing very little resemblance to the processes they’re supposedly modeling] because physiologically implausible parameter values may be required to compute operationally useful procedures.”¹

Probabilistic Approach to Generating Decompression Profiles

In 2018, David Doolette, Greg Murphy, and Wayne Gerth published a paper with a large set of iso-risk decompression tables for heliox CCR dives with a constant PO₂ of 1.3 to depths of up to 90 m/300 ft. Because the algorithm used to generate the Navy tables (called LEM-he8n25) was too complex to run on wrist-worn dive computers at the time, the researchers had to find a way to emulate its outputs with something simpler—a modified Thalmann algorithm with only three tissue compartments (10, 22, and 202 minutes). 

The key difference from conventional approaches is that instead applying a set of model parameters that are deemed to be “safe” (or safe enough), they instead used the acceptable level of DCS risk as input to compute optimal (i.e., as short as possible) decompression schedules that remained within the specified DCS risk limits (2.3%, 4%, and 5% for the tables in this study).

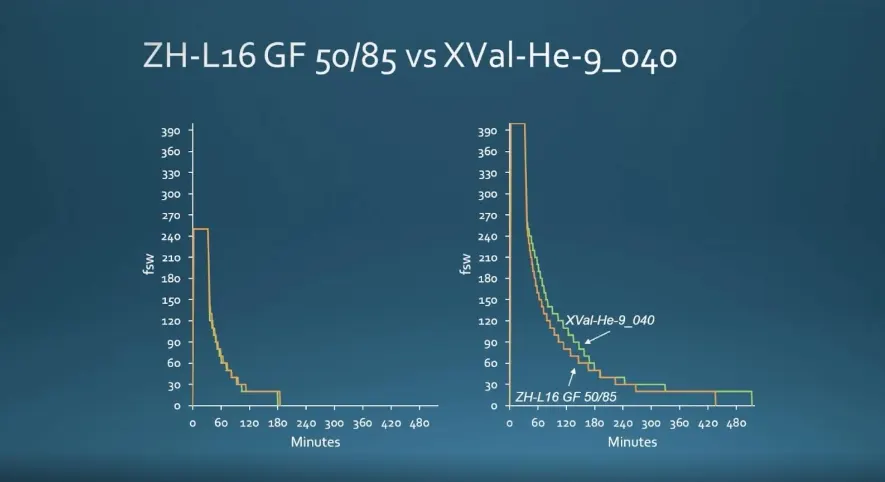
Why are iso-risk decompression algorithms of interest to tech and cave divers?

As outlined by Doolette, decompression schedules generated by conventional algorithms carry an unquantified risk of DCS that escalates with the magnitude of the dive. While this may not be very relevant for the majority of dives—even technical ones—for bigger dives, it clearly is. The 30-minute, 70-meter profile on the left in fig. 4 above (where the Bühlmann 50/85 profile and the Thalmann profile for a 4% DCS risk are nearly identical) might give readers a rough idea of where Bühlmann and Thalmann begin to diverge. The ability to quantify and control this risk could be a major gain.

There are considerations: While there is more and better data available for military diving than for its civilian counterpart (and a lot of the research we rely on for our evolving understanding of decompression physiology comes from the military), Navy diving procedures are quite different from what civilian divers are used to in terms of mission criticality, workload, breathing gas choices, and closed circuit rebreather (CCR) setpoints, to name a few. The Thalmann algorithm has solid empirical support for the types of dives Navy divers do, but it hasn’t been tested as extensively in the civilian domain.

Moreover, civilian divers generally do not have a hyperbaric chamber available on the boat or in the back of their truck in case they come up bent, and they rarely have to worry about things like enemy action or depth charges that might provide an increased incentive to get out of the water as quickly as possible. Given these circumstances, it stands to reason that civilian divers ought to dive no less conservatively than the Navy.

Yet if one compares the 120-meter profiles above (right side of fig. 4), the Bühlmann 50/85 profile is the more aggressive of the two, and the Thalmann profile still carries a DCS risk of 4% despite being an hour longer.² The risk of the Bühlmann profile hasn’t been quantified, but it’s safe to assume that it would be deemed too aggressive by military standards. To quote David Doolette, “I know which one I’d rather dive.”

With the above in mind, there may be a case for exploring the potential of iso-risk (probabilistic), Thalmann-based deco for use in civilian tech and cave diving.

Can I try it?

There are no Thalmann-based dive computers or desktop applications currently available to the general public. While the Navy currently uses Shearwater computers with an implementation of the Thalmann algorithm. [Ed note: Shearwater replaced Cochran Undersea Technology computers, after the company was shut down following founder Mike Cochran’s death] These aren’t commercially available at present—not for reasons of confidentiality (the algorithm itself has been published, and there are no restrictions to implementing it on dive computers), but for lack of market demand. [Ed. note: Maybe if we all asked Shearwater nicely—Josh are you listening? ]

For an impression, in addition to the constant-PO₂ tables published by Doolette, Murphy, and Gerth in their 2018 paper, the CCR dive tables for 300 ft and shallower in the U.S. Navy Diving Manuals are Thalmann-based and iso-risk. At least one Global Underwater Explorers (GUE) tech instructor and software engineer, California-based Beto Nava has programmed the Thalmann algorithm on his laptop to generate probabilistic deco schedules. “Some divers complain about the length of decompression required to reduce the risk on deep dives,” he offered.

Time will tell whether explorers at the very top of our field—those who regularly perform deep dives with long bottom times—will begin to integrate a probabilistic approach to decompression as proposed by Doolette into their practice. For the rest of us, I hope that this article provides an interesting glimpse into the research that tries to define the boundary between dives that could conceivably be done under certain circumstances, and those that simply shouldn’t be done under any circumstances at all.

Thanks are owed to Dr. Greg Murphy, Research Engineer at the US Navy Experimental Diving Unit, for a number of crucial details and corrections. His help has been invaluable. All remaining errors are mine. TBl.

Footnotes: 

1. With fellow hyperbaric research legend Bill Hamilton, in: Bennett and Elliott’s Physiology and Medicine of Diving (Brubakk et. al., 5th ed., 2003, ch. 10-2, Decompression Practice, p. 455) 
2. To generate a Bühlmann profile of similar length, one would have to apply a GF high of about 50. The linear off-gassing kinetics give Thalmann profiles a particular shape that is difficult to emulate with gradient factors.###

DIY Thalmann

Here are the resources IT tech-savvy readers (like Nava) need to implement the Thalmann algorithm on their own devices. This is public information from the Defense Technical Information Center. Please note that there are also a selection of usable tables for various depths and times in the appendix of the second paper. Check them out.

 Thalmann Algorithm Decompression Table Generation Software Design Document by Wayne Gerth (2010)

 Thalmann Algorithm Parameter Sets For Support Of Constant 1.3 Atm Po2 He-O2 Diving To 300 Fsw by David Doolette, Greg Murphy & Wayne Gerth (2018)

Here are some notes to help you better understand the Thalmann implementation: Notes from a Tech Instructor and Coder by Beto Nava

Variable Gradient Model: An Approach To Create More Efficient Decompressions (2019) British tech pioneer and inventor Kevin Gurr has been building dive computers since the early 1990s, including the world’s first mixed gas diving computer, the VR3, which he launched in 1997, through his former company VR Technology Ltd. based in Dorset, UK. He also designed and built three sport rebreathers. Now the Maritime Technology Officer at Avon Protection managing military rebreathers, Gurr discusses an innovative modification of gradient factors that he developed for use with his various devices.

DIVE DEEPER

RF4: Advances in Decompression Theory and Practice by David Doolette

NEDU: Computer Algorithms Used in Computing the Mk 15/16 Constant 0.7 ATA Oxygen Partial Pressure Decompression Tables. By Thalmann, Edward D

InDEPTH: NEDU Deep Stop Summary by Jarrod Jablonski

InDEPTH: They Helped Foment a Dive Computing Revolution: RIP Cochran Undersea Technology (1986-2020) By Carlos E. Lander

Alert Diver: Deep in the Science of Diving by Michael Menduno

Shearwater Blog: On The EDGE—The First Electronic Dive Computers  by Michael Menduno

InDEPTH: The Early Days of Technical Trimix Diving: Understanding Special Tables: Some Things You Should Know  by Dr. R.W. “Bill” Hamilton 

Tim Blömeke teaches technical and recreational diving in Taiwan and the Philippines. He is also a freelance writer and translator, as well as a member of the editorial team of Alert Diver. For questions, comments, and inquiries, you can contact him via his blog page or on Instagram.